Voir la table des matières Ne plus voir la table des matières
Un arbre Verkle est un schéma d’engagement qui fonctionne de manière similaire à un arbre Merkle, mais a des témoins beaucoup plus petits. Cela fonctionne en remplaçant les hachages dans un arbre Merkle par un engagement vectoriel, ce qui rend les facteurs de branchement plus larges plus efficaces.
Merci à Kevaundray Wedderburn pour ses commentaires sur la publication.
Aperçu
Pour plus de détails sur le fonctionnement des arbres verkle, voir :
Le but de cet article est d’expliquer la mise en page concrète du projet d’arbre de verkle EIP. Il s’adresse aux développeurs clients qui souhaitent implémenter des arbres verkle et recherchent une introduction avant d’approfondir l’EIP.
Les arbres Verkle introduisent un certain nombre de changements dans l’arborescence. Les changements les plus significatifs sont :
- un passage des clés de 20 octets aux clés de 32 octets (à ne pas confondre avec les adresses de 32 octets, ce qui est un changement séparé) ;
- la fusion du compte et des tentatives de stockage ; et enfin
- L’introduction du verkle trie lui-même, qui utilise des engagements vectoriels au lieu de hachages.
Comme schéma d’engagement vectoriel pour l’arbre de verkle, nous utilisons Les engagements de Pedersen. Les engagements de Pedersen sont basés sur des courbes elliptiques. Pour une introduction aux engagements de Pedersen et comment les utiliser comme engagements polynomiaux ou vectoriels à l’aide d’Inner Product Arguments, voir ici.
La courbe que nous utilisons est Bandersnatch. Cette courbe a été choisie parce qu’elle est performante, et aussi parce qu’elle permettra aux SNARK efficaces dans BLS12_381 de raisonner sur l’arbre de verkle à l’avenir. Cela peut être utile pour les cumuls et permettre une mise à niveau où tous les témoins peuvent être compressés dans un seul SNARK une fois que cela devient pratique, sans avoir besoin d’une mise à jour d’engagement supplémentaire.
L’ordre de courbe/taille de champ scalaire de bandersnatch est $p = 13108968793781547619861935127046491459309155893440570251786403306729687672801$, qui est un nombre premier de 253 bits. En conséquence, nous ne pouvons nous engager en toute sécurité que sur des chaînes de bits d’au plus 252 bits, sinon le champ déborde. Nous avons choisi un facteur de branchement (largeur) de 256 pour l’arbre verkle, ce qui signifie que chaque engagement peut s’engager jusqu’à 256 valeurs de 252 bits chacune (ou pour être précis, des entiers jusqu’à $p – 1$). Nous écrivons cela sous la forme $mathrm{Commit}(v_0, v_1, …, v_{255})$ pour s’engager dans la liste $v$ de longueur 256.
Disposition de l’arbre verkle
L’un des objectifs de conception avec l’EIP d’arbre verkle est de rendre les accès aux positions voisines (par exemple le stockage avec presque la même adresse ou des morceaux de code voisins) peu coûteux d’accès. Pour ce faire, une clé est constituée d’un tige de 31 octets et un suffixe d’un octet pour un total de 32 octets. Le schéma de clé est conçu de manière à ce que les emplacements de stockage « proches » soient mappés sur la même tige et un suffixe différent. Pour plus de détails, veuillez consulter le projet EIP.
L’arbre verkle lui-même est alors composé de deux types de nœuds :
- Nœuds d’extension, qui représentent 256 valeurs avec le même radical mais des suffixes différents
- Nœuds internes, qui ont jusqu’à 256 enfants, qui peuvent être d’autres nœuds internes ou des nœuds d’extension.
L’engagement envers un nœud d’extension est un engagement envers un vecteur à 4 éléments ; les positions restantes seront 0. C’est $C = mathrm{Commit}(1, mathrm{stem}, C_1, C_2)$
C₁ et C₂ sont deux autres engagements qui s’engagent sur toutes les valeurs dont le radical est égal à $mathrm{stem}$. La raison pour laquelle nous avons besoin d’engagements est que les valeurs ont 32 octets, mais nous ne pouvons stocker que 252 bits par élément de champ. Un seul engagement ne suffirait donc pas à stocker 256 valeurs. Ainsi, à la place, C₁ stocke les valeurs pour le suffixe 0 à 127, et C₂ stocke 128 à 255, où les valeurs sont divisées en deux afin de s’adapter à la taille du champ (nous y reviendrons plus tard.)
L’extension ainsi que les engagements C₁ et C₂ sont appelés « arbre d’extension et de suffixe » (EaS en abrégé).
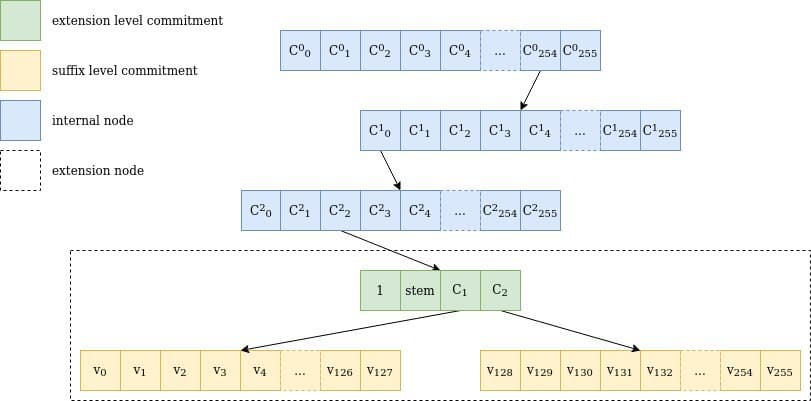
Figure 1 Représentation d’une promenade à travers un arbre verkle pour la clé 0xfe0002abcd..ff04: le chemin passe par 3 nœuds internes avec 256 enfants chacun (254, 0, 2), un nœud d’extension représentant abcd..ff et les deux engagements d’arbre de suffixes, y compris la valeur pour 04, v₄. Notez que $texttt{stem}$ est en fait les 31 premiers octets de la clé, y compris le chemin à travers les nœuds internes.
Engagement envers les valeurs nœuds feuilles
Chaque nœud d’arbre d’extension et de suffixe contient 256 valeurs. Parce qu’une valeur a une largeur de 256 bits et que nous ne pouvons stocker que 252 bits en toute sécurité dans un élément de champ, quatre bits seraient perdus si nous essayions simplement de stocker une valeur dans un élément de champ.
Pour contourner ce problème, nous avons choisi de partitionner le groupe de 256 valeurs en deux groupes de 128 valeurs chacun. Chaque valeur de 32 octets dans un groupe est divisée en deux valeurs de 16 octets. Donc une valeur $v_i in mathbb{B}{32}$ est transformé en $v^text{(inférieur)}{i} in mathbb{B}{16}$ et $v^text{(supérieur)}{i} in mathbb{B}{16}$ tel que $v^text{(inférieur)}{i} ++ v^text{(supérieur)}_{i} = v_i$.
Un « marqueur de feuille » est ajouté au $v^text{(lower)}{i}$, pour différencier une feuille qui n’a jamais été consultée et une feuille qui a été écrasée par des 0. Aucune valeur n’est jamais supprimée d’un arbre verkle. Cela est nécessaire pour les prochains régimes d’expiration de l’État. Ce marqueur est défini au 129e bit, c’est-à-dire $v^text{(lower,modified)}{i} = v^text{(inférieur)}{i} + 2^{128}$ si vᵢ a déjà été accédé, et $v^text{(inférieur, modifié)}{i} = 0$ si vᵢ n’a jamais été accédé.
Les deux engagements C₁ et C₂ sont alors définis comme
Engagement des nœuds d’extension
L’engagement envers un nœud d’extension est composé d’un « marqueur d’extension », qui n’est que le numéro 1, les deux engagements de sous-arbre C₁ et C₂, et le tige de la clé menant à ce nœud d’extension.
$C = mathrm{Commit}(1, mathrm{stem}, C_1, C_2)$
Contrairement aux nœuds d’extension de l’arbre Merkle-Patricia, qui ne contiennent que la section de la clé qui relie le nœud interne parent au nœud interne enfant, la tige couvre l’intégralité de la clé jusqu’à ce point. En effet, les arbres de verkle sont conçus avec des preuves sans état à l’esprit : si une nouvelle clé est insérée qui « divise » l’extension en deux, l’aîné n’a pas besoin d’être mis à jour, ce qui permet une preuve plus petite.
Engagement des nœuds internes
Les nœuds internes ont la méthode de calcul la plus simple pour leurs engagements : le nœud est vu comme un vecteur de 256 valeurs, qui sont la (représentation de champ de l’) engagement racine de chacun de leurs 256 sous-arbres. L’engagement pour un sous-arbre vide est de 0$. Si le sous-arbre n’est pas vide, alors l’engagement pour le nœud interne est
$C = mathrm{Commit}(C_0, C_1, …, C_{255})$
où les Cᵢ sont les enfants du nœud interne, et 0 si un enfant est vide.
Insertion dans l’arbre
La figure 2 est une illustration du processus d’insertion d’une nouvelle valeur dans l’arbre, ce qui devient intéressant lorsque les tiges entrent en collision sur plusieurs octets initiaux.
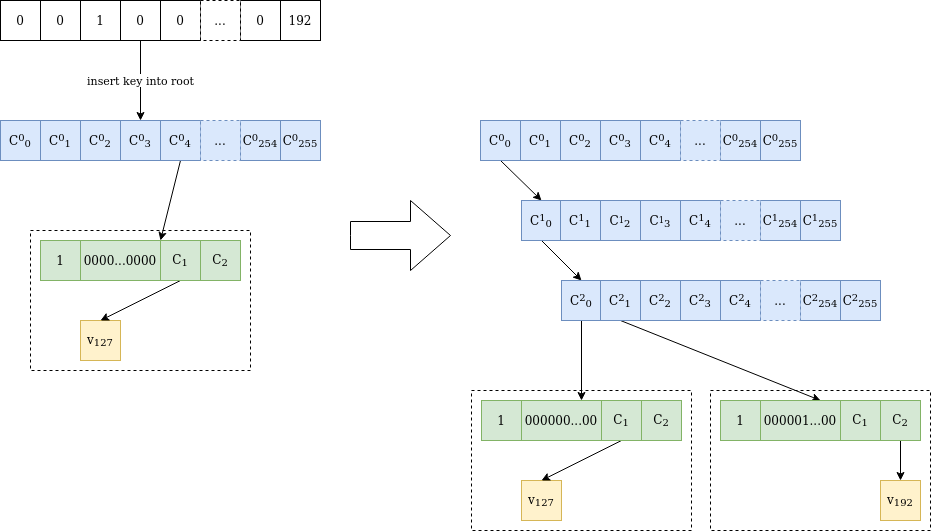
Figure 2 La valeur v₁₉₂ est insérée à l’emplacement 0000010000...0000 dans un arbre de verkle contenant uniquement la valeur v₁₂₇ à l’emplacement 0000000000...0000. Étant donné que les tiges diffèrent au troisième octet, deux nœuds internes sont ajoutés jusqu’à l’octet différent. Ensuite, un autre arbre « extension et suffixe » est inséré, avec une racine complète de 31 octets. Le nœud initial est intact et $C^2_0$ a la même valeur que $C^0_0$ avant l’insertion.
Arbres moins profonds, épreuves plus petites
La structure arborescente verkle crée des arbres moins profonds, ce qui réduit la quantité de données stockées. Son véritable pouvoir, cependant, vient de sa capacité à produire des preuves plus petites, c’est-à-dire des témoins. Cela sera expliqué dans le prochain article.
